He aquí el segundo artículo de la serie publicada en El Tamiz cuántica sin fórmulas, en esta ocasión se trata de el efecto fotoeléctrico.
El efecto fotoeléctrico
Tras realizar un pequeño preludio y hablar sobre la hipótesis de Planck, continuamos hoy la serie de Cuántica sin fórmulas hablando acerca del segundo paso que derrumbaría las suposiciones de la física clásica y revolucionaría la física del siglo XX aún más que la relatividad. Este segundo paso, como veremos, se basa en el primero, y tiene ciertos paralelismos con él. Me refiero al efecto fotoeléctrico.
Este efecto era uno de los pocos fenómenos que no tenían una correcta explicación teórica a finales del siglo XIX (lo mismo que la radiación de cuerpo negro, de la que ya hablamos y que Planck logró justificar mediante su hipótesis), y consiste en lo siguiente: si se coge un trozo de un metal y se hace incidir luz sobre él, a veces la luz es capaz de arrancar electrones del metal y hacer que se muevan, produciendo así una corriente eléctrica – de ahí el nombre del efecto, “electricidad producida con luz”. Pero la clave está en el “a veces”, y ahí es donde los físicos se mesaban los cabellos con preocupación.
Los científicos se dedicaron, por supuesto, a pensar por qué se producía y cuándo debería producirse el efecto fotoeléctrico (que debería involucrar partes de la ciencia bien desarrolladas como el electromagnetismo), y la teoría clásica razonaba de la siguiente manera:
La luz transporta energía. Cuando la luz choca contra el metal, le transfiere energía. Si esa energía es suficiente para arrancar electrones, se produce el efecto fotoeléctrico, y si no es suficiente, no ocurre nada. De manera que si, por ejemplo, apunto una bombilla muy tenue contra una chapa de metal, no se produce efecto fotoeléctrico, pero si aumento la potencia de la bombilla mil veces, se producirá el efecto.
Pero esto no pasaba. Si la bombilla tenue no era capaz de producir el efecto fotoeléctrico, entonces por mucho que aumentara la intensidad de la luz, diez, mil, un millón de veces, no salía ni un solo electrón del metal. También pasaba al revés, claro: si la bombilla era capaz de arrancar electrones del metal, era posible disminuir su potencia todo lo que se quisiera: incluso un debilísimo rayo de luz de la bombilla era capaz de arrancar electrones – arrancaba menos electrones que la luz potente, pero los arrancaba. Y esto no tenía absolutamente ningún sentido.
¿De qué dependía entonces que se produjera el efecto, si no era de la intensidad de la luz? Los científicos, por muy tercos que fueran tratando de explicar las cosas con la teoría clásica, son científicos: se dedicaron a cambiar otras condiciones del experimento hasta llegar a una conclusión absurda, imposible, totalmente inaceptable – el factor que decidía que se arrancaran electrones era el color de la luz de la bombilla. Dicho en términos más técnicos era la frecuencia de la radiación, pero nuestros ojos “ven” la frecuencia de la luz como el color, de modo que nos vale con eso.
Es decir, que si cogiéramos una bombilla cuyo color pudiéramos hacer variar siguiendo los colores del arco iris (los físicos de la época iban más allá de la luz visible, pero una vez más nos vale con esto), desde el rojo al violeta, al principio no se producía el efecto. Pero llegaba un momento, que dependía del metal que se tratase (y no dependía para nada de la intensidad de la luz) en el que empezaban a arrancarse electrones – supongamos que al llegar al amarillo. Si se seguía variando el color a lo largo del arco iris, cualquier color pasado el amarillo en ese recorrido (por ejemplo, el violeta) también arrancaba electrones.
La intensidad de la luz sí tenía cierto efecto, como hemos dicho: si un rayo de luz roja (por ejemplo) no producía el efecto, por muy intensa que fuera la luz no ocurría nada. Pero si un rayo de luz amarilla sí lo producía, entonces al aumentar la intensidad de la luz aumentaba el número de electrones arrancados. Sin embargo, incluso esto no encajaba con la teoría clásica: aumentaba el número de electrones arrancados (la intensidad de la corriente), pero no la energía de cada electrón (el voltaje de la corriente), que era absolutamente igual para la luz amarilla independientemente de la intensidad. Es decir, si la luz amarilla producía electrones con una determinada energía cada uno, multiplicar la intensidad de la luz por cien hacía que salieran cien veces más electrones del metal, pero todos con la misma energía que cuando salían menos. La verdad es que era desesperante.
Pero es que la cosa no acaba ahí: la frecuencia (el color) de la luz no sólo determinaba si se producía el efecto o no. Además, la energía de cada electrón (que ya hemos dicho no dependía de la intensidad) aumentaba según la frecuencia de la luz aumentaba. Es decir, que si se usaba luz azul, los electrones tenían más energía que si se usaba luz amarilla. Pero ¿qué demonios tenía que ver el color de la luz con la energía de los electrones?
La solución la dio el siempre genial Albert Einstein, quien, recordemos, ya había apuntado a la hipótesis de Planck como la solución teórica al problema de la radiación de cuerpo negro. Einstein aplicó el razonamiento lógico y extrajo una conclusión inevitable de la hipótesis de Planck – aplicar la lógica y extraer conclusiones eran cosas en las que Einstein era un genio sin igual. El razonamiento del alemán fue el siguiente:
Si los pequeños osciladores que componen la materia sólo pueden tener unas energías determinadas, unos “escalones de energía” que son proporcionales a la constante de Planck y a la frecuencia con la que oscilan, ¿cómo será la energía que absorben y desprenden? La luz, al fin y al cabo, sale de estos osciladores. Una bombilla, por ejemplo, brilla porque los átomos del filamento están muy calientes y desprenden energía electromagnética, que ellos mismos pierden. Pero si los osciladores pierden energía, no pueden perder una cantidad arbitraria: deben “bajar la escalera” de energía y, como mínimo, perder un “escalón”. De forma inevitable, la energía luminosa que desprenden no puede ser arbitraria, tiene que estar hecha de estos “escalones”.

Einstein en 1905, cuando publicó su explicación del efecto fotoeléctrico.
Si lo piensas, es totalmente lógico (aunque generó una gran polémica al principio): si las fuentes de luz sólo pueden estar en los escalones de energía que propuso Planck, y cuando emiten luz es porque pierden energía, la luz que emiten debe estar hecha de esos “escalones”. No es posible emitir una cantidad arbitrariamente pequeña de energía luminosa: sólo puede tenerse luz “en píldoras”. La luz está cuantizada.
Naturalmente, un físico que se precie no habla de “píldoras”, “escalones” o “trozos” de luz. Einstein llamó a este concepto Lichtquant, “cuanto de luz”. En 1926, Gilbert Lewis propuso otro nombre, que es el que usamos hoy en día: fotón. Durante el resto de este artículo hablaremos de fotones, aunque Einstein no los mencionara en la publicación en la que propuso su existencia.
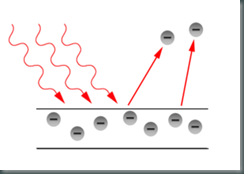
Cuando se considera el efecto fotoeléctrico en términos de fotones, todo tiene sentido: la luz que llega al metal está compuesta de fotones. Cada uno de ellos tiene una energía proporcional a la constante de Planck y la frecuencia de la radiación. Si la luz es muy intensa (una bombilla muy grande y potente), hay muchos fotones. Si la luz cambia de color pero no de intensidad, hay el mismo número de fotones, pero cada uno tiene más energía (hacia el azul) o menos energía (hacia el rojo).
Cuando uno de estos fotones llega al metal y choca con un electrón, puede darle su energía: si esta energía es suficiente para arrancarlo del metal, se produce el efecto fotoeléctrico, y si no es suficiente, no pasa nada. La cuestión es que la interacción se produce entre un fotón y un electrón – no entre “toda la luz” y “todos los electrones”, porque tanto la luz como la materia están cuantizadas. ¿De qué depende entonces de que se produzca el efecto? De la frecuencia de la luz, es decir, del color. Si es luz roja (por ejemplo), cada fotón tiene muy poca energía. Tal vez haya muchísimos fotones, pero a este electrón en particular sólo le afecta el que ha chocado contra él, y éste no tiene suficiente energía para arrancarlo, de modo que no sucede nada.
Si se tiene luz con una gran frecuencia (por ejemplo, azul), cada fotón tiene mucha energía: proviene de un “escalón grande” de Planck. Cuando choca con un electrón puede darle suficiente energía para arrancarlo del metal, y entonces se produce el efecto fotoeléctrico. Claro, si esta luz azul es muy intensa (hay muchos fotones), y cada uno arranca un electrón, se arrancarán muchos electrones, exactamente como sucede en la realidad. Pero si cada fotón no hubiera tenido suficiente energía para arrancar a su electrón, por muchos fotones que hubiera, no pasaría nada en absoluto.
Puede que te preguntes, querido lector, Vale, pero ¿no puede el electrón recibir un fotón con poca energía, “guardarse la energía” que le ha dado el fotón, aunque no sea bastante, y esperar al siguiente fotón, y así hasta tener suficiente energía para escapar?
No, no y mil veces no – recuerda la hipótesis de Planck. Si un fotón no tiene suficiente energía para arrancar el electrón es porque el escalón de energía es demasiado alto. Un electrón no puede tener “un poquito más de energía” arbitrariamente: o tiene la que tiene ahora, o tiene la del siguiente escalón. Si el fotón no tiene suficiente energía para arrancar el electrón es que la energía del siguiente escalón es demasiado alta, de modo que el electrón ni siquiera puede almacenar la energía del fotón, porque lo pondría “entre dos escalones”. De modo que se queda exactamente como estaba antes, por muchos fotones de poca energía que le lleguen. Estos fotones, al no poder ser absorbidos por el electrón, continúan su camino, y probablemente acabarán dando su energía a algún átomo, haciéndolo vibrar más rápidamente (es decir, calentando el metal), pues los “escalones” son ahí más pequeños que los necesarios para arrancar el electrón.
Y, por supuesto, si la luz tiene una frecuencia altísima, los electrones arrancados tendrán una gran energía (y la corriente, un gran voltaje): el fotón tiene mucha energía, y gasta parte de ella en arrancar el electrón. El resto se la queda el electrón, pues el fotón ha desaparecido: un fotón es un “escalón”, y no puede romperse y dar parte de su energía. O está, o no está. Cuando le da su energía al electrón, se da entero. El electrón, entonces, tiene mucha energía. Mientras que si la frecuencia de la luz es sólo la necesaria para arrancar al electrón y nada más, el electrón tiene muy poca energía. Una vez más, coincidía a la perfección con los experimentos.
Pero la teoría de Einstein no sólo coincidía con la realidad cualitativamente, sino que era capaz de realizar predicciones cuantitativas: si la energía de cada fotón era proporcional a la constante de Planck y a la frecuencia de la luz, entonces la energía de los electrones arrancados debería aumentar proporcionalmente a la frecuencia de la luz. Aunque cueste creerlo, en 1905, cuando Einstein publica su propuesta, aún no se había medido cuantitativamente la energía de los electrones arrancados. En 1915, Robert Andrews Millikan realizó experimentos muy precisos: la energía de los electrones aumentaba de forma lineal con la frecuencia, exactamente lo que Einstein había predicho.
Parte de la comunidad científica aún se resistía a aceptar la existencia del Lichtquant, pero una vez más, aceptando una idea aparentemente absurda y contraria a la intuición (que la luz está hecha de “trozos”), los experimentos se explicaban con una precisión indiscutible. Albert Einstein recibió el Premio Nobel en 1921 por su explicación del efecto fotoeléctrico, siguiendo los pasos de Planck – y, como él, muy reacio a aceptar las implicaciones posteriores de su teoría, de las que hablaremos en artículos posteriores en la serie.
La pregunta inmediata, por supuesto, es: si la luz está hecha de pequeños paquetes, ¿por qué la vemos de forma continua? Nadie ve “trocitos” de luz, no, y la respuesta (que ya deberías saber, si has entendido la serie hasta ahora) es que son demasiado pequeños. Si recuerdas la hipótesis de Planck, la energía de cada escalón es minúscula y, por lo tanto, la energía de cada fotón es igualmente minúscula. Cuando nos llega, por ejemplo, la luz del Sol, está hecha de fotones, pero cada segundo llegan a nuestro ojo unos veinte trillones de fotones: 20.000.000.000.000.000.000 fotones. ¿Pero cómo vamos a distinguir que no es un “chorro” de energía sino un “goteo”? Es imposible.
La explicación de Einstein del efecto fotoeléctrico tiene implicaciones profundas sobre nuestro concepto del Universo: la luz era, para la comunidad científica, clara e indiscutiblemente una onda, como el sonido o las olas. Sufría fenómenos, como la interferencia y la difracción, que sólo sufren las ondas. Sin embargo, ahora llegaba Einstein y decía que la luz estaba compuesta de lo que, a efectos prácticos, eran pequeñas partículas… ¿cómo podía la luz sufrir difracción si estaba hecha de fotones? Pero ¿cómo podía la luz producir el efecto fotoeléctrico si no estaba hecha de fotones? La solución de Einstein generaba preguntas aún más difíciles de responder: ¿era la luz una onda o partículas?
La solución, por supuesto, es el tercer paso en nuestra caída de la realidad objetiva, y el responsable fue otro genio del razonamiento lógico: el francés Louis-Victor-Pierre-Raymond, séptimo Duque de Broglie (normalmente conocido como Louis de Broglie).















